Xem bảng tổng hợp công thức lượng giác đầy đủ dễ thuộc, dễ nhớ

Công thức lượng giác là nội dung kiến thức quan trọng trong chương trình toán học, thường được áp dụng nhiều trong các bài thi học kỳ, thi tốt nghiệp, thi đánh giá năng lực… của học sinh trung học phổ thông. Tuy nhiên, lượng kiến thức về lượng giác khá lớn, đòi hỏi các em phải đầu tư thời gian để học, ghi nhớ và rèn luyện thành thạo các dạng bài tập liên quan. Trong bài viết dưới đây, UK Academy sẽ tổng hợp công thức lượng giác đầy đủ để giúp học sinh dễ thuộc, dễ ghi nhớ và áp dụng hiệu quả trong quá trình giải các bài tập toán.

>> Tham khảo thêm:

• Công thức đạo hàm sơ cấp, cao cấp và đạo hàm lượng giác đầy đủ
• Công thức, cách tính diện tích hình tròn đầy đủ, chi tiết
• Nguyên tử khối là gì? Cách để ghi nhớ bảng nguyên tử khối hoá học đầy đủ nhất

Khái niệm về tỉ số lượng giác

Tỉ số lượng giác của một góc nhọn là  khái niệm trong lượng giác, dùng để thể hiện mối liên hệ giữa các cạnh và góc trong tam giác vuông. Tỉ số này được ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, từ toán học thuần túy cho đến vật lý, kỹ thuật, thậm chí cả thiên văn học. 

Xét trường hợp một tam giác vuông ta có công thức sau:

• Sin: Là tỉ số giữa độ dài cạnh đối và cạnh huyền của góc
• Cos: Là tỉ số giữa độ dài cạnh kề và cạnh huyền của góc
• Tan: Là tỉ số giữa độ dài cạnh đối và cạnh kề của góc
• Cot: Là tỉ số giữa độ dài cạnh kề và cạnh đối của góc

Mẹo học thuộc: “Sin đi học, Cos không học, Tan đoàn kết, Cot kết đoàn”

Tính ứng dụng công thức lượng giác

• Bài toán hình học phẳng và không gian: Các dạng công thức lượng giác như định lý sin và định lý cos được sử dụng để tính toán chiều dài cạnh, góc và diện tích tam giác, đặc biệt là tam giác không vuông. 
• Giải phương trình lượng giác: Các phương trình có chứa các hàm lượng giác như sin, cos, tan được giải bằng cách áp dụng công thức lượng giác liên quan để đơn giản hóa và tìm nghiệm.
• Chế tạo và thiết kế kỹ thuật: Trong lĩnh vực kỹ thuật, công thức lượng giác giúp xác định lực, gia tốc và chuyển động trong cơ học. 
• Vật lý: Các công thức lượng giác được sử dụng để mô tả sóng điện từ, sóng âm và các hiện tượng dao động khác. 
• Thiên văn học: Sử dụng công thức lượng giác để tính toán vị trí của ngôi, các hành tinh và hiện tượng thiên văn khác thông qua các góc và khung thời gian.
• Điện tử và viễn thông: Phân tích tín hiệu và truyền thông số dựa nhiều vào lượng giác trong quá trình giải mã, điều tiết và truyền tải tín hiệu.

Các công thức lượng giác cơ bản và công thức cộng lượng giác

>> Xem thêm

• 10 phương pháp học toán hiệu quả giúp học sinh đạt điểm cao
• 101+ bài toán tư duy cho trẻ 5 tuổi hay và phù hợp
• Toán tư duy là gì? Những điều cần biết về môn toán tư duy cho trẻ

6 công thức lượng giác cơ bản:

5 công thức cộng lượng giác:

Mẹo học thuộc: “Sin thì sin cos cos sin, cos thì cos cos sin sin dấu trừ. Tan thì tan nọ tan kia chia cho mẫu số 1 trừ tan tan.”

Công thức lượng giác của các cung liên kết bên trên đường tròn lượng giác

Trường hợp 2 cung đối nhau

Công thức lượng giác 2 cung đối nhau là một công thức quan trọng trong lượng giác, hữu ích trong việc giải những bài toán lượng giác và xác định giá trị của các cung trong tương quan hình học và vật lý. 

• cos (-x) = cos x
• sin (-x) = -sin x
• tan (-x) = -tan x
• cot (-x) = -cot x

Trường hợp 2 cung bù nhau

Công thức lượng giác 2 cung bù nhau thường được áp dụng cho các cung có tổng 2 góc bằng π hoặc bằng 180 độ. Có 2 phép tính lượng giác hai cung đối nhau chính cho sin và cos, từ  đó phát triển thêm công thức cho tan và cot.

• sin (π – x) = sin x
• cos (π – x) = -cos x
• tan (π – x) = -tan x
• cot (π – x) = -cot x

Trường hợp 2 cung phụ nhau

Công thức lượng giác 2 cung phụ nhau áp dụng cho 2 góc có tổng bằng 90 độ hoặc π/2 radian. 

• sin (π/2 – x) = cos x
• cos (π/2– x) = sin x
• tan (π/2 – x) = cot x
• cot (π/2 – x) = tan x

Trường hợp 2 cung hơn, kém π

Công thức lượng giác 2 cung hơn kém π (180 độ) được áp dụng cho các góc có hiệu của chúng bằng π. 

• sin (π + x) = -sin x
• cos (π + x) = -cos x
• tan (π + x) = tan x
• cot (π + x) = cot x

Trường hợp 2 cung hơn kém π/2

Công thức lượng giác 2 cung hơn kém π/2 (hay 90 độ) áp dụng cho các góc có hiệu của chúng bằng π/2. 

• sin (π/2 + x) = cos x
• cos (π/2 + x) = -sin x
• tan (π/2 + x) = -cot x
• cot (π/2 + x) = -tan x

Công thức nhân đôi, nhân ba, nhân bốn lượng giác

Các công thức nhân lượng giác này được dùng để đơn giản hóa và tính toán những giá trị lượng giác nhân 2, nhân 3 hoặc nhân 4 của một góc dựa vào giá trị lượng giác của góc ban đầu.

Công thức lượng giác nhân đôi

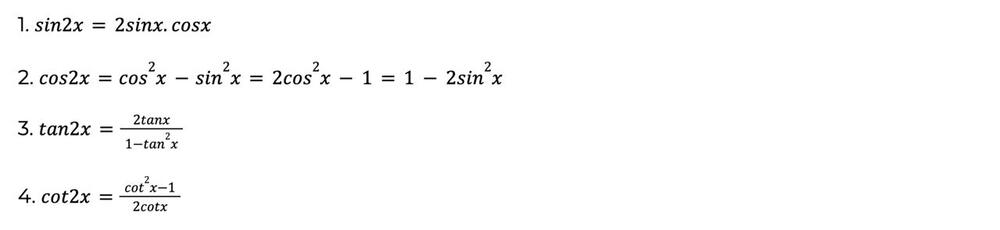
Công thức lượng giác nhân ba

Công thức lượng giác nhân bốn

Công thức hạ bậc lượng giác

Các công thức hạ bậc lượng giác đều được biến đổi từ công thức lượng giác cơ bản.

Công thức lượng giác biến tích thành tổng

Trong chương trình toán học trung học phổ thông, các em học sinh cần nắm chắc các công thức lượng giác biến đổi tích thành tổng sau:

Công thức lượng giác biến tổng thành tích

Các công thức này chuyển đổi tổng hoặc hiệu của 2 hàm lượng giác thành tích của các hàm lượng giác khác, giúp đơn giản hóa các biểu thức lượng giác và hỗ trợ tính toán phương trình lượng giác phức tạp. 

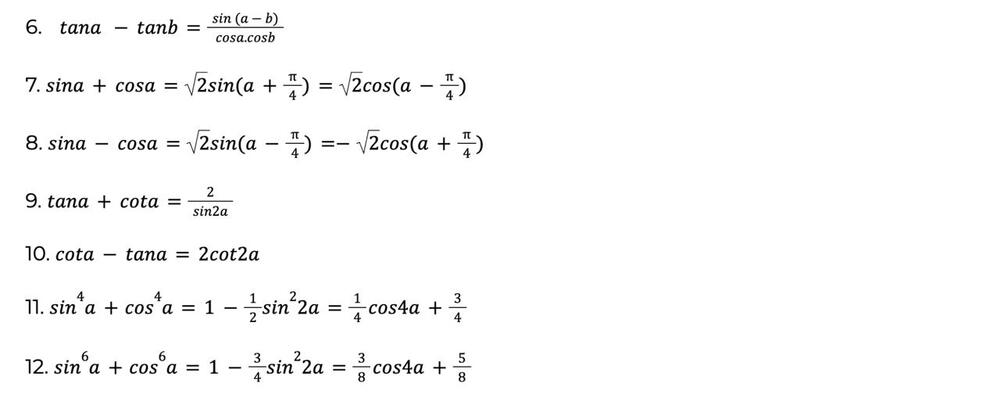
Các công thức nghiệm của phương trình lượng giác

Công thức nghiệm với phương trình lượng giác cơ bản

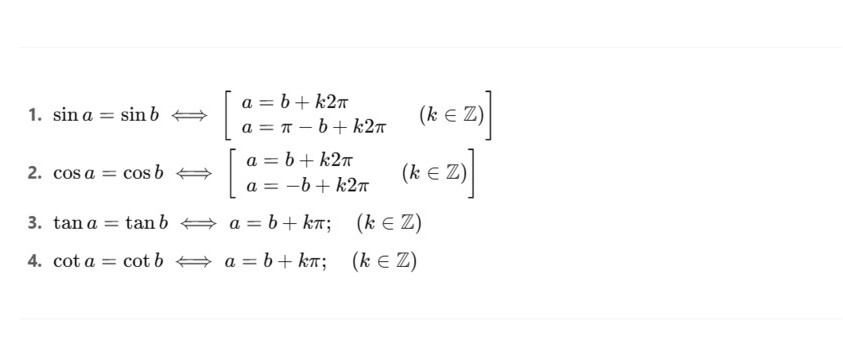
Công thức nghiệm của phương trình lượng giác đặc biệt

Các công thức nghiệm của phương trình lượng giác trong trường hợp đặc biệt gồm:

• sin a = 0 ⇔ a = kπ; (k ∈ Z)
• sin a = 1 ⇔ a = π/2 + k2π; (k ∈ Z)
• sin a = -1 ⇔ a = -π/2 + k2π; (k ∈ Z)
• cos a = 0 ⇔ a = π/2 + kπ; (k ∈ Z)
• cos a = 1 ⇔ a = k2π; (k ∈ Z)
• cos a = -1 ⇔ a = π + k2π; (k ∈ Z)

Công thức lượng giác nâng cao

Bên cạnh các công thức lượng giác cơ bản, các em học sinh cũng cần học thêm các công thức lượng giác nâng cao để mở rộng kiến thức, giúp làm các bài tập trong bài thi để đạt điểm cao hơn.

Các công thức lượng giác đặc biệt:

Hàm lượng giác ngược:

Lượng giác hóa số phức:

Tích vô hạn ứng dụng với hàm lượng giác đặc biệt:

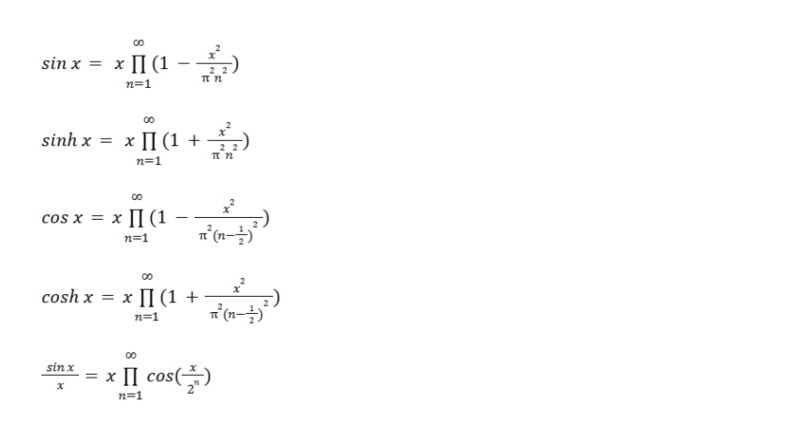
Mẹo hay giúp ghi nhớ nhanh các công thức lượng giác

Công thức lượng giác là nội dung kiến thức cốt lõi xuất hiện trong các bài kiểm tra, bài thi quan trọng, nhưng nhiều bạn học sinh lại gặp khó khăn trong việc học và ghi nhớ. Dưới đây là một số bí quyết giúp ghi nhớ nhanh những công thức lượng giác các em học sinh có thể tham khảo và áp dụng.

>> Có thể tham khảo thêm:

• Cách học môn Ngữ văn hiệu quả giúp học sinh tự tin thi tốt, đạt điểm giỏi
• 10 Phương pháp học toán hiệu quả giúp học sinh đạt điểm cao
• Thì hiện tại đơn (Simple Present): Công thức, cách dùng và bài tập có lời giải chi tiết

Bài thơ ghi nhớ công thức lượng giác

Sin thì sin cos cos sin sin

Cos thì cos  cos sin sin rồi trừ

Tan tổng thì lấy tổng tan

Chia 1 trừ với tích tan dễ mà.

                                   (Nguồn: Sưu tầm)

Bài thơ ghi nhớ công thức về tan tổng

Tan 2 tổng 2 tầng cao rộng

Trên thượng tầng tan cộng cùng tan

Hạ tầng số 1 rất ngang tàng

Dám trừ đi cả tan tan anh hùng.

                               (Nguồn: Sưu tầm)

Các câu thơ giúp nhớ nhanh giá trị lượng giác của những cung liên kết đặc biệt

Câu thơ giúp nhớ nhanh giá trị lượng giác của các cung liên kết đặc biệt “Cos đối, sin bù, phụ chéo, tan hơn kém pi”.

                                                                                                                                                                   (Nguồn: Sưu tầm)

Câu thơ giúp nhớ nhanh công thức lượng giác biến tổng thành tích và tích thành tổng

Cos cộng cos bằng 2 cos cos

cos trừ cos bằng trừ 2 sin sin

Sin cộng sin bằng 2 sin cos

sin trừ sin bằng 2 cos sin.

Sin thì sin cos cos sin

Cos thì cos cos sin sin “coi chừng” (dấu trừ).

Tang tổng thì lấy tổng tang

Chia một trừ với tích tang dễ dàng.

                                                 (Nguồn: Sưu tầm)

Câu thơ ghi nhớ công thức lượng giác nhân đôi, nhân ba

Câu thơ học công thức lượng giác nhân đôi: 

Sin gấp đôi bằng 2 sin cos

Cos gấp đôi bằng bình phương cos trừ đi bình sin

Bằng trừ 1 cộng 2 bình cos

Bằng cộng 1 trừ 2 bình sin.

                                       (Nguồn: Sưu tầm)

Thơ vui học thuộc công thức lượng giác nhân ba:

Nhân ba một góc bất kỳ

sin thì ba bốn, cos thì bốn ba

dấu trừ đặt giữa 2 ta

lập phương chỗ bốn thế là ok

Tang đôi ta lấy đôi tang (2 tang)

Chia 1 trừ lại bình tang, ra liền.

                                        (Nguồn: Sưu tầm)

Hy vọng rằng bài viết này giúp các em  dễ dàng ghi nhớ công thức lượng giác, nắm vững và áp dụng thành thạo vào ác bài tập lượng giác, từ đó chuẩn bị tốt cho các kỳ thi sắp tới. Ngoài ra, các em học sinh cũng có thể vào chuyên mục Tin tức của UK Academy để cập nhập thêm nhiều kiến thức hữu ích khác.