Công thức tính đạo hàm sơ cấp, cao cấp và đạo hàm lượng giác đầy đủ

Trong chương trình môn Toán của bậc Trung học phổ thông, đạo hàm là một trong những phần kiến thức quan trọng liên quan đến cả quá trình học và các kỳ thi lớn. Chính vì thế, việc nắm vững công thức đạo hàm sẽ giúp học sinh giải bài tập toán nhanh chóng, hiệu quả. Nhằm giúp các bạn ôn luyện dễ dàng hơn, UK Academy sẽ tổng hợp những công thức đạo hàm cơ bản đến nâng cao cùng các ví dụ minh họa qua bài viết dưới đây.

Định nghĩa đạo hàm là gì?

Trong toán học giải tích, đạo hàm là một hàm mô tả sự biến thiên tại một điểm hay tỷ số giữa số gia của hàm số và số gia của đối số tại 1 điểm bất kỳ gọi là x0. Trong đó, độ lớn của biến thiên và chiều của biến thiên thể hiện giá trị của đạo hàm.

Theo một định nghĩa khác, đạo hàm được hiểu là sự biến thiên lên xuống của hàm số tại điểm thay đổi. Theo đó, đạo hàm của hàm y=f(x) sẽ được ký hiệu là f′(x0) hoặc y′(x0). Cụ thể như sau:

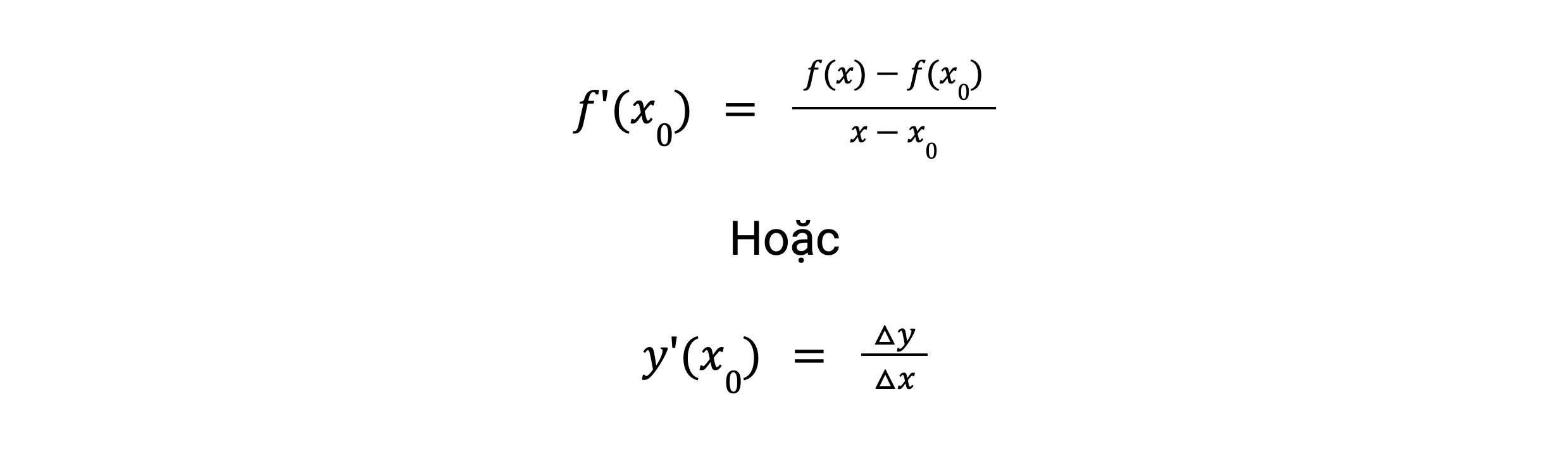
Trong đó: 

• Số gia của đối số là Δx = x − x0
• Số gia của hàm là Δy = y − y0

Quy tắc tính đạo hàm theo định nghĩa

Khi áp dụng công thức đạo hàm để tính toán và giải các bài tập toán học, các bạn học sinh cần rõ quy tắc đạo hàm dựa trên định nghĩa như sau: 

• Bước 1: Giả sử Δx là gia số của x tại x0, lúc này ta tính Δy = f(x0 + Δx) – f(x0).
• Bước 2: Thực hiện lập tỉ số giữa ΔyΔx.
• Bước 3: Tính giới hạn của ΔyΔx khi Δx0ΔyΔx.

Tuy nhiên các bạn cần lưu ý, nếu thay x0 với x thì có quy tắc tính hàm số là y = f(x) với x ∈ (a;b).

Tính liên tục và sự tồn tại của đạo hàm trong toán học có mối quan hệ như thế nào?

Nếu hàm số có dạng y = f(x), đạo hàm x0 thì sẽ liên tục tại x0. Để chứng minh điều này ta xét hàm số y = f(x) = |x|. Tại điểm x0 = 0 ta có f(0) = 0 và x0f(x) = x0f|x| = 0. Như vậy, ta có thể thấy hàm số đã liên tục tại điểm x = 0.

Ngoài ra, ta có:

• Δy = f(x0 + Δx) – f(0) = |Δx| => ΔyΔx = |Δx|Δx
• ΔyΔx = {1 khi Δx > 0 và -1 khi Δx < 0

Vì thế, Δx0 + ΔyΔx = 1 và Δx0 – ΔyΔx = -1 => Δx0ΔyΔx không tồn tại. Hàm số y = |x| không có đạo hàm tại x0 = 0.

Tổng hợp các công thức đạo hàm cần nhớ cho học sinh các cấp

Dưới đây là tổng hợp đầy đủ các công thức đạo hàm để giúp các bạn học sinh dễ dàng tra cứu và áp dụng giải các bài tập liên quan.

Bảng công thức tính đạo hàm đầy đủ

Bảng công thức đạo hàm lượng giác

Bảng công thức đạo hàm và nguyên hàm

Bảng công thức đạo hàm của hàm số, biến số và phân thức hữu tỉ

Bảng công thức tính đạo hàm cao cấp thường gặp

Các dạng bài tập liên quan đến đạo hàm

Thường xuyên luyện tập các bài tập liên quan đến đạo hàm sẽ giúp học sinh ghi nhớ kiến thức và giải bài tập thành thạo. Để giúp quá trình học và giải bài tập của học sinh trở nên dễ dàng, ghi nhớ lâu hơn, UK Academy đã tổng hợp các dạng toán và bài tập đạo hàm chi tiết dưới đây.

Dạng bài tập số 1: Tính đạo hàm theo định nghĩa

Trong các bài tập đạo hàm, dạng toán tính đạo theo định nghĩa là đơn giản nhất, bởi vì chỉ cần vận dụng định nghĩa và áp dụng các công thức cơ bản để tính toán. Ví dụ:

Dạng bài tập số 2: Viết phương trình tiếp tuyến khi được cho trước hệ số góc

Dạng bài tập này yêu cầu viết phương trình tiếp tuyến Δ của (C) : y = f( x ), cho biết Δ có hệ số góc là k. Phương pháp giải dạng bài này, trước tiên gọi M(x0 ; y0) là tiếp điểm, sau đó tính y’ => y'(x0). Theo đó, phương trình tiếp tuyến Δ có hệ số góc k => y’ = (x0 ) = k (i) và x0 => y0 = f(x0) => Δ : y = k (x – x0 )+ y0.

Dạng bài tập số 3: Chứng minh những đẳng thức liên quan đến đạo hàm

Với dạng bài tập này, học sinh được yêu cầu chứng minh những đẳng thức liên quan tới đạo hàm dựa trên các điều kiện có sẵn. Để giải dạng toán này, học sinh cần tính toán, chứng minh các đẳng thức liên quan đến đạo hàm sao cho chính xác và đưa ra kết quả.

Dạng bài tập số 4: Viết phương trình tiếp tuyến khi biết tiếp điểm

Đây cũng là một trong số các dạng bài tập áp dụng công thức đạo hàm phổ biến. Trong đề bài thường sẽ cho một phương trình tiếp tuyến của đồ thị đường cong (C): y = f(x), với một tiếp điểm M(x0;y0) cho sẵn có dạng y = y’(x0)(x – x0) + y0. Cuối cùng, học sinh chỉ cần thay thế các dữ kiện cho sẵn và tính toán để tìm ra đáp án.

Dạng bài tập số 5: Giải phương trình và bất phương trình có chứa đạo hàm

Để giải dạng bài tập tìm phương trình và bất phương trình có chứa đạo hàm, học sinh cần áp dụng kết hợp nhiều công thức đạo hàm và nguyên hàm để tìm ra kết quả chính xác.

Dạng bài tập số 6: Sử dụng công thức nguyên hàm, đạo hàm

Với dạng bài tập này đòi hỏi học sinh vừa phải nắm chắc các công thức đạo hàm và nguyên hàm, vừa phải hiểu bản chất của chúng. Trong quá trình giải những đề bài có hàm số phức tạp, học sinh cần lưu ý rút gọn hàm số trước rồi mới áp dụng công thức đạo hàm ln, nhất là các bài tập liên quan đến lượng giác.

Dạng bài tập số 7: Tính đạo hàm cao cấp

Dạng bài tập này thường áp dụng công thức tính đạo hàm cấp 2 trở lên, vậy nên học sinh muốn tính chính xác đạo hàm y’ cấp cao thì cần sử dụng công thức y(n) = (y(n-1))’. Bên cạnh đó, học sinh cũng cần thực hiện tính lần lượt đạo hàm từ cấp 1, 2, 3, 4… rồi mới suy luận ra công thức đạo hàm cấp n.

Cách giải các bài tập đạo hàm nhanh và hiệu quả

Đạo hàm là nội dung kiến thức không đơn giản, do đó nhiều bạn học sinh gặp khó khăn trong việc ghi nhớ bảng công thức đạo hàm và tìm cách giải các bài toán liên quan. Dưới đây là một số bí quyết giúp các em học sinh giải quyết những bài tập đạo hàm một cách nhanh chóng và hiệu quả.

Nắm chắc định nghĩa và công thức tính đạo hàm

Để có thể giải các bài toán đạo hàm nhanh chóng và chính xác, học sinh cần nắm vững kiến thức lý thuyết như định nghĩa, công thức tính, quy tắc cơ bản,… Không nên học vẹt mà phải hiểu rõ bản chất, phân tích thật kỹ định nghĩa, định lý, đồng thời kết hợp làm nhiều dạng bài tập khác nhau để biết cách vận dụng công thức hiệu quả.

Giải lần lượt các bài tập đạo hàm từ cơ bản đến nâng cao thường xuyên

Khi đã nắm chắc công thức, học sinh hãy thường xuyên luyện giải đề sẽ giúp ghi nhớ công thức lâu, biết được phương pháp giải nhanh, từ đó tiết kiệm thời gian khi làm bài. Bài tập liên quan đến đạo hàm rất nhiều dạng, hãy bắt đầu từ những bài tập cơ bản để lấy động lực, khi đã nhuần nhuyễn thì tiếp tục chinh phục các dạng đề nâng cao như đạo hàm từ định nghĩa, tiếp tuyến đồ thị, đạo hàm cao cấp,… để nâng cao kỹ năng giải toán.

Chú ý các điều kiện của hàm số

Các bài toán về đạo hàm sẽ luôn có điều kiện cho trước để học sinh đi tìm nghiệm. Thế nhưng, nhiều bạn lại thường bỏ qua bước tìm điều kiện của hàm số nên dẫn đến kết quả sai. Vì vậy, hãy luôn nhớ xác định điều kiện của hàm số trước khi giải bất cứ dạng bài nào để cho ra kết quả chính xác.

Luôn ghi chú lại các lỗi sai và tự rút kinh nghiệm xuyên suốt quá trình làm bài tập

Trong quá trình làm bài tập, chắc chắn sẽ có lúc bạn giải sai hoặc không tìm ra đáp án. Đây là lúc bạn cần ghi chú lại các lỗi sai, tham khảo góp ý từ bạn bè hay thầy cô để tìm ra công thức tính nhanh, mẹo nhận biết dạng bài tập,…để áp dụng một cách tốt nhất.

Chăm chỉ và kiên trì luyện tập thường xuyên qua bài tập, đề thi

Để thành thạo các công thức, điều quan trọng là phải chăm chỉ và kiên trì luyện tập nhiều bài tập và đề thi. Hãy sắp xếp thời gian giải các dạng bài tập cơ bản trong sách giáo khoa, đề cương, tiếp đến là mở rộng ra các kiến thức nâng cao và luyện các dạng đề thi. Chắc chắn rằng với sự chăm chỉ và kiên trì, bạn có thể nắm được 80 – 90% kiến thức, từ đó việc giải các bài tập đạo hàm sẽ trở nên dễ dàng và chính xác hơn rất nhiều.

Một số bài tập về các công thức đạo hàm có lời giải đầy đủ

Sau đây là một số bài tập về các công thức đạo hàm có lời giải đầy đủ, giúp các bạn rèn luyện kỹ năng giải toán hiệu quả:

Bài 1: Cho một hàm số y = x3 + 3mx2 + (m + 1)x + 1 (1), với m là một tham số thực. Hãy tìm các giá trị của m để tiếp tuyến của đồ thị của hàm số có hoành độ x = -1 và đi qua điểm A (1; 2).

Bài giải:

TXD: Đ = R

y’ = f’ (x) = 3 x 2 + 6mx + m + 1

Với x0 = -1 => y0 = 2m – 1, f’ (-1) = -5m + 4

Phương trình tiếp tuyến tại M (-1; 2m – 1), y = (-5m + 4) (x + 1) +2m – 1 (d)

Ta có: A (1; 2) ∈ (d) ⇔ 2(-5m + 4) + 2m – 1 = 2 => m = 5/8

Bài 2: Cho hàm số (C): y = x3 + 3 x 2 – 9x + 5. Tìm tiếp tuyến có hệ số góc nhỏ nhất trong tất cả các tiếp tuyến của đồ thị (C).

Bài giải:

Ta có: y’ = f’(x) = 3 x 2 + 6x – 9

Gọi x0 là hoành độ tiếp điểm của tiếp tuyến, vậy f’(0) = 3 x 02 + 6 x 0 – 9

Ta có: 3 x 02 + 6 x 0 – 9 = 3 (x02 + 2 x 0 + 1) – 12 = 3 (x0 + 1) 2 – 12 > -12

Vậy min f(x0) = -12 tại x0 = -1 => y0 = 16

=> Phương trình tiếp tuyến  (C) cần tìm y = -12 (x + 1) + 16 ⇔ y = -12x + 4

Hy vọng rằng với hệ thống công thức đạo hàm rõ ràng, dễ hiểu được UK Academy tổng hợp trên đây sẽ giúp các bạn học sinh nắm vững kiến thức, hỗ trợ quá trình học tập, ôn thi đạt kết quả cao. Đừng quên dành thời gian luyện tập đa dạng các dạng bài để củng cố kiến thức và nâng cao kỹ năng giải toán. UK Academy chúc các bạn học tập thật tốt và tự tin chinh phục mọi kỳ thi.