Công thức, cách tính diện tích hình tròn chi tiết 2025
Công thức tính diện tích hình tròn là kiến thức vô cùng quan trọng trong toán học, ứng dụng rộng rãi từ bài tập trên lớp đến thực tế như thiết kế, xây dựng. Bài viết hôm nay, UK Academy sẽ mách bạn công thức tính diện tích hình tròn và cách tính diện tích theo chu vi, đường kính,… kèm ví dụ minh hoạ dễ hiểu, giúp các em học sinh dễ dàng áp dụng kiến thức vào bài tập hiệu quả nhất.
Quý phụ huynh có thể liên hệ trực tiếp với Trường Quốc tế Song ngữ Học viện Anh Quốc ngay hôm nay để có cơ hội trải nghiệm và hiểu rõ hơn về chương trình đào tạo của trường:
>> Tham khảo thêm:
- Nguyên tử khối là gì? Bảng nguyên tử khối hóa học mới và đầy đủ nhất
- Công thức tính đạo hàm sơ cấp, cao cấp và đạo hàm lượng giác đầy đủ
- Bảng cửu chương nhân chia từ 1 đến 10: Cách học nhanh thuộc và nhớ lâu
Các lý thuyết cơ bản về hình tròn
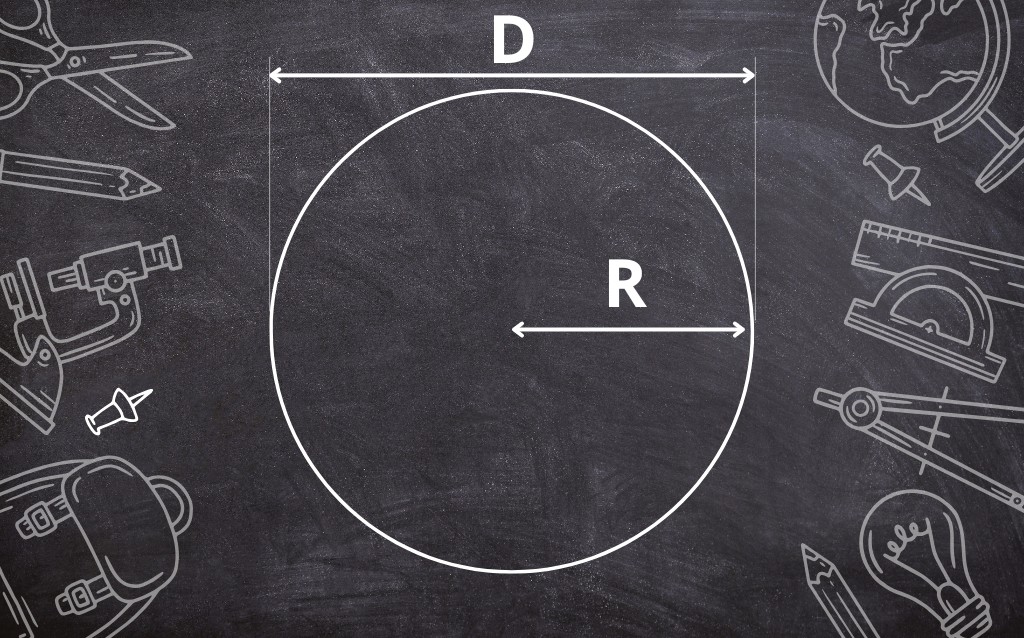
Hình tròn là tập hợp tất cả các điểm nằm trên một mặt phẳng và cách đều một điểm cố định (gọi là tâm) ở cùng một khoảng cách xác định (gọi là bán kính). Đặc biệt là để hình thành một hình tròn, bán kính phải có giá trị lớn hơn 0. Trước khi tìm hiểu công thức diện tích hình tròn, các em học sinh cần biết được những tính chất đặc trưng của hình học này.
- Tâm: Là điểm cố định và nằm ở giữa của hình tròn, được ký hiệu là (x, y) trong hệ tọa độ hai chiều.
- Bán kính: Khoảng cách từ tâm đến bất kỳ điểm nào thuộc hình tròn và được ký hiệu là r.
- Đường kính: Được ký hiệu là d, là một đoạn thẳng đi qua tâm của hình tròn, chia hình tròn thành hai nửa. Chiều dài đường kính sẽ gấp đôi bán kính, có nghĩa là d = 2r.
- Đối xứng: Hình tròn có tính chất đối xứng tuyệt đối tại tâm, có nghĩa là nếu bạn vẽ một đoạn thẳng từ tâm đến bất kỳ điểm nào trên hình tròn thì sẽ chia hình tròn thành hai nửa đối xứng với nhau.
- Tính chất Pythagoras: Trong một hình tam giác vuông, nếu cạnh huyền của tam giác là đường kính của một hình tròn thì cạnh góc vuông của tam giác chính là bán kính của hình tròn.
- Quan hệ với hình vuông và hình chữ nhật: Hình tròn có thể nằm gọn trong một hình vuông có cạnh bằng đường kính hoặc một hình chữ nhật có chiều rộng bằng bán kính và chiều dài bằng đường kính.
>> Có thể bố mẹ quan tâm:
- 10 Phương pháp học toán hiệu quả giúp học sinh đạt điểm cao
- Cách học môn Ngữ văn hiệu quả giúp học sinh tự tin thi tốt, đạt điểm giỏi
- Toán tư duy là gì? Những điều cần biết về môn toán tư duy cho trẻ
Công thức tính diện tích hình trong theo chương trình chuẩn
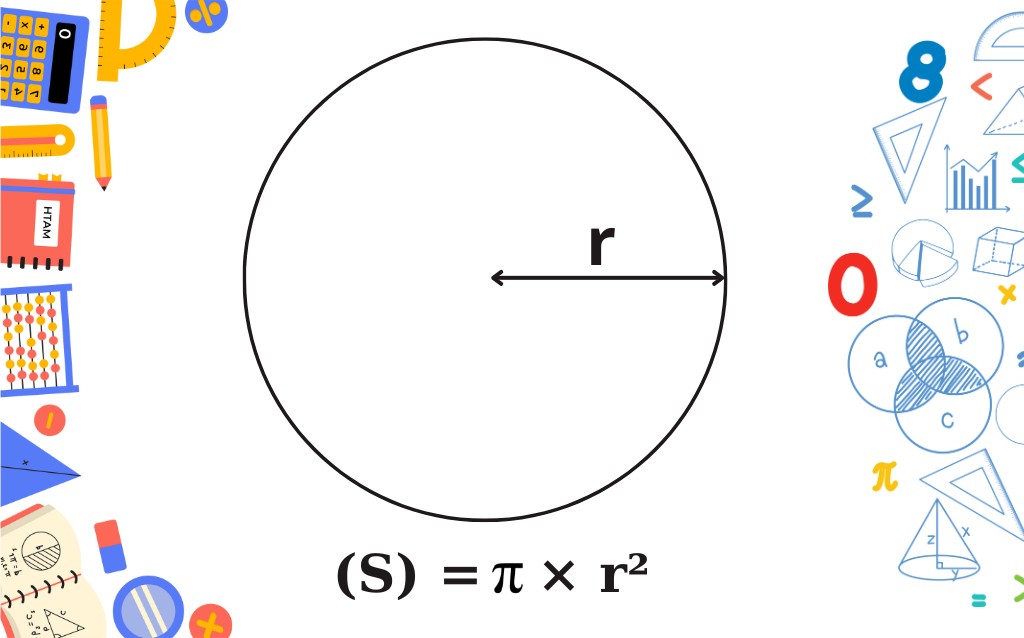
Để tính diện tích hình tròn, học sinh hãy áp dụng công thức sau:
Diện tích (S) = π × r²
Trong đó:
- S là diện tích của hình tròn, được tính bằng đơn vị diện tích như mét vuông (m²) hoặc centimet vuông (cm²).
- π (Pi) là một hằng số toán học xấp xỉ khoảng 3,14159.
- r là bán kính của hình tròn và phải có giá trị lớn hơn 0.
Ví dụ: Tính diện tích hình tròn có bán kính (r) 4cm.
Thay giá trị r = 4cm vào công thức trên, ta có S = 3,14 × 4² => S ≈ 50.24 cm²
Vậy diện tích của hình tròn có bán kính 4 cm là khoảng 50.24 cm².
>> Xem thêm: 101+ Bài tập toán tư duy cho trẻ 5 tuổi hay và phù hợp
Các cách tính diện tích hình tròn
Có nhiều cách tính diện tích hình tròn có thể áp dụng vào trong quá trình học và giải bài tập. Sau đây là hướng dẫn cách tính diện tích hình tròn khi đã biết đường kính, chu vi và bán kính của hình tròn.
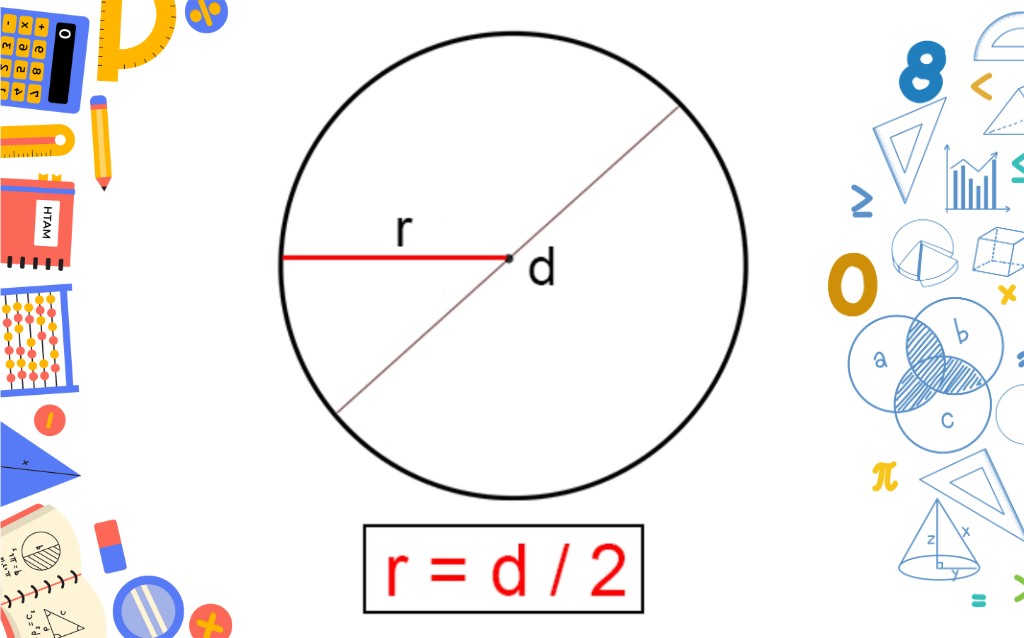
Tính diện tích hình tròn khi có đường kính (d)
Công thức tính diện tích hình tròn khi có đường kính cho trước như sau: S = π(d / 2)²
Khi đề bài toán cho sẵn đường kính (d), học sinh chỉ cần áp dụng vào công thức ở trên là hoàn thành. Một cách tính khác nữa là hãy tìm bán kính của hình tròn (r=d/2), sau đó áp dụng kết quả vừa tính vào công thức S = π x r² cũng sẽ ra kết quả chính xác.
Ví dụ: Nếu biết đường kính (d) của hình tròn là 14 cm, ta tính diện tích như sau:
S = 3,14 x (14 / 2)²
=> S = 3,14 × 7²
=> S ≈ 153,86 cm²
Tính diện tích hình tròn khi biết chu vi (C)
Nếu muốn tính diện tích hình tròn khi biết chu vi (C), học sinh hãy sử dụng công thức S = C² / 4π. Trong đó:
- S là diện tích hình tròn
- C là chu vi hình tròn
- π là một hằng số xấp xỉ khoảng 3,14159
Ví dụ: Nếu biết chu vi của hình tròn là 20 cm, ta tính diện tích như sau:
S = 20² / (4 x 3,14)
=> S ≈ 31,84 cm²
Cách tính S hình tròn khi biết bán kính (r)
Công thức tính diện tích hình tròn khi biết bán kính (r) sẽ giống với công thức chính vừa được chia sẻ trên là: S = π x r². Trong đó, π là một hằng số thường được sử dụng là 3,14. Do đó, học sinh chỉ cần biết bán kính (r) đã có thể dễ dàng áp dụng công thức trên và có được kết quả chuẩn xác.
>> Có thể bố mẹ quan tâm:
- Giáo dục toàn diện là gì? Những yếu tố giáo dục toàn diện cho trẻ
- Chương trình tích hợp là gì? Có nên cho con học chương trình tích hợp?
Một số bài tập tính diện tích hình tròn điển hình không thể bỏ qua
Dựa trên các công thức ở trên, các em học sinh có thể dễ dàng giải được hầu hết các bài tập tính diện tích hình tròn. Tuy nhiên, hãy tham khảo thêm các dạng bài tập thường gặp trong các bài kiểm tra, bài thi dưới đây để biết cách làm nhanh và chính xác nhất.
Bài tập tính S hình tròn cơ bản khi biết đường kính d và bán kính r
Với bài tập này, học sinh chỉ cần áp dụng công thức S = π x r² để tính diện tích của hình tròn nếu cho biết bán kính (r). Trong trường hợp đề bài cho biết đường kính (d), học sinh hãy áp dụng công thức r = d/2 để tính độ dài của bán kính, sau đó mới áp dụng công thức tính diện tích hình tròn.
Ví dụ: Cho hình tròn C có đường kính d = 20 cm. Hãy tính diện tích hình tròn C?
Giải: Ta có, bán kính bằng một nửa đường kính theo công thức là r = d/2
=> r = 20/2 = 10 cm
S = π x r² = 3,14 x 10² = 314 cm²
Dạng bài tính đường kính và bán kính của hình tròn khi biết diện tích
Khi biết diện tích của hình tròn, học sinh có thể tính được bán kính (r) và đường kính (d) của hình tròn bằng các công thức sau:
- Tính bán kính (r) từ diện tích (S): Bán kính (r) = √(S / π)
- Tính đường kính (D) từ diện tích (S): Đường kính (d) = 2 × bán kính (r) = 2 × √(S / π)
Ví dụ: Nếu biết diện tích của hình tròn (S) là 100 cm², ta tính bán kính và đường kính như sau:
Bán kính (r) = √(100 cm² / 3,14)
=> r ≈ 5.64 cm
Đường kính (d): = 2 × bán kính (r)
=> D = 2 × 5.64 cm ≈ 11.28 cm
Vậy khi diện tích của hình tròn là 100 cm² thì bán kính là khoảng 5.64 cm và đường kính là khoảng 11.28 cm.
Công thức tính diện tích hình tròn trong ngôn ngữ lập trình pascal
Pascal là ngôn ngữ lập trình mà các em học sinh được học trong chương trình Tin học lớp 8 và lớp 11. Trong đó, tính diện tích hình tròn là một dạng thường xuyên xuất hiện trong đề bài. Để sử dụng π trong Pascal, học sinh có thể sử dụng hằng số đã được định nghĩa sẵn trong thư viện Math hoặc tự định nghĩa hằng số π nếu cần.
Sau đây là hướng cách tính diện tích hình tròn trong Pascal:
program TinhDienTichHinhTron;
const
π = 3.14159; // Giá trị xấp xỉ của π
var
banKinh, dienTich: Real;
begin
// Nhập bán kính từ người dùng
Write(‘Nhập bán kính của hình tròn: ‘);
ReadLn(banKinh);
// Tính diện tích của hình tròn
dienTich := Pi * sqr(banKinh);
// Hiển thị kết quả
WriteLn(‘Diện tích của hình tròn là: ‘, dienTich:0:2);
end.
Trong đoạn mã này sẽ yêu cầu người dùng nhập bán kính của hình tròn, sau đó tính và hiển thị diện tích của hình tròn. Lưu ý, bạn đã sử dụng hàm `sqr` để tính bình phương của bán kính và `:0:2` để định dạng hiển thị diện tích với hai chữ số thập phân.
Cách tính diện tích hình tròn ngoại tiếp hình vuông ABCD
Để tính diện tích hình tròn ngoại tiếp, các bạn cần biết chiều dài cạnh của hình tròn vuông ngoại tiếp hoặc đường chéo của hình vuông ngoại tiếp của hình tròn. Hình tròn ngoại tiếp là hình tròn được vẽ sao cho tiếp xúc với tất cả các cạnh của hình vuông tại những điểm tiếp xúc.
Để tính diện tích hình tròn ngoại tiếp, hãy áp dụng công thức S = (Đường chéo)²/2. Trong đó, đường chéo là chiều dài cạnh của hình tròn vuông ngoại tiếp và cũng chính là đường kính của hình tròn. Điều này có nghĩa là học sinh cần tìm đường chéo (đường kính) của hình tròn vuông ngoại tiếp trước khi thực hiện tính diện tích hình tròn ngoại tiếp.
Các dạng bài tập tính diện tích hình tròn tham khảo có lời giải đầy đủ
Dưới đây là một số bài tập tính diện tích hình tròn có lời giải đầy đủ, các bạn có thể tham khảo để hiểu hơn về cách áp dụng các công thức tính S.
Bài tập 1: Tính diện tích hình tròn khi có đường kinh d
Đề bài: Tính diện tích của hình tròn khi biết đường kính là 10 cm.
Bài giải:
Tính bán kính (r) từ đường kính (d) theo công thức r = d/2
=> r = 10/2 = 5
Áp dụng công thức tính diện tích hình tròn S = π x r²
=> S = π × 5²
=> S = 3,14 × 25
=> S ≈ 78,50 cm²
Bài tập 2: Tính diện tích hình tròn khi có bán kính r
Đề bài: Tính diện tích của hình tròn khi biết bán kính là 8 cm.
Bài giải:
Ta có bán kính (r) = 6 cm
Áp dụng công thức tính diện tích hình tròn S = π x r²
=> S = π × 8²
=> S = 3,14 x 64
=> S ≈ 200,96 cm²
Bài tập 3: Cho chu vi hình tròn, tính bán kính của hình tròn đó
Đề bài: Tìm bán kính của hình tròn khi biết chu vi là 30 cm.
Bài giải:
Sử dụng công thức tính bán kính từ chu vi: r = C/(2π)
=> r = 30/(2 x 3,14)
=> r ≈ 3,18 cm
Bài tập 4: Tính diện tích của hình tròn ngoại tiếp
Đề bài: Cho một hình vuông có cạnh là 10 cm. Hãy tính diện tích của hình tròn ngoại tiếp hình vuông này.
Bài giải:
Ta có, đường kính (d) của hình tròn ngoại tiếp bằng cạnh của hình vuông.
=> d = 10 cm
Bán kính (r) của hình tròn ngoại tiếp bằng một nửa đường kính (d).
=> r = d/2
=> r = 10/2 = 5 cm
Áp dụng công thức tính diện tích hình tròn S = π x r²
=> S = π × 4²
=> S = 3.14 × 16
=> S ≈ 50.24 cm²
Trên đây là tổng hợp các công thức tính diện tích hình tròn chi tiết nhất cùng một số dạng bài tập điển hình, dễ gặp trong quá trình học Toán. UK Academy hy vọng bài viết đã mang đến cho các em nguồn tài liệu hữu ích, giúp củng cố kiến thức và có thể áp dụng thành thạo trong mọi dạng đề.
>> Tham khảo thêm:
- Bảng chữ cái tiếng Việt 29 chữ theo chuẩn Bộ Giáo dục & Đào tạo mới nhất
- Bảng chữ cái tiếng Anh: Cách phát âm và phiên âm chính xác nhất
- 7+ Bảng chữ in hoa tiếng Việt đẹp, sáng tạo, thu hút nhất
Khám phá thêm về UKA Academy







